In this lesson, we will explore the dynamics of option pricing and delve into the risk-reward profiles associated with different types of trades.
As a brief recap from our previous lesson, it's important to note that the Greeks do not dictate an option's price; rather, they provide insights into potential changes in the premium (or price) of an option.
Fundamentally, the price you pay for an option is influenced by market forces of supply and demand, akin to any other commodity you purchase, be it groceries or cars. Market dynamics always determine the price.
While an options pricing model may offer a theoretical value, it is essential to recognize that the real value of an option is dictated by the market. The pricing model considers six key components: changes in the underlying stock price, the option's strike price, time to expiration, implied volatility, and dividends.
One of the most commonly used formulas for estimating theoretical value is the Black-Scholes Option Pricing Model, upon which many other pricing models are based.
The formula for calculating the theoretical value of a call option is depicted as shown in the provided image.
Through understanding these variables and the theoretical value, traders can gauge the approximate fair value of an option. Most trading platforms conveniently provide this theoretical value, eliminating the need for manual calculations.
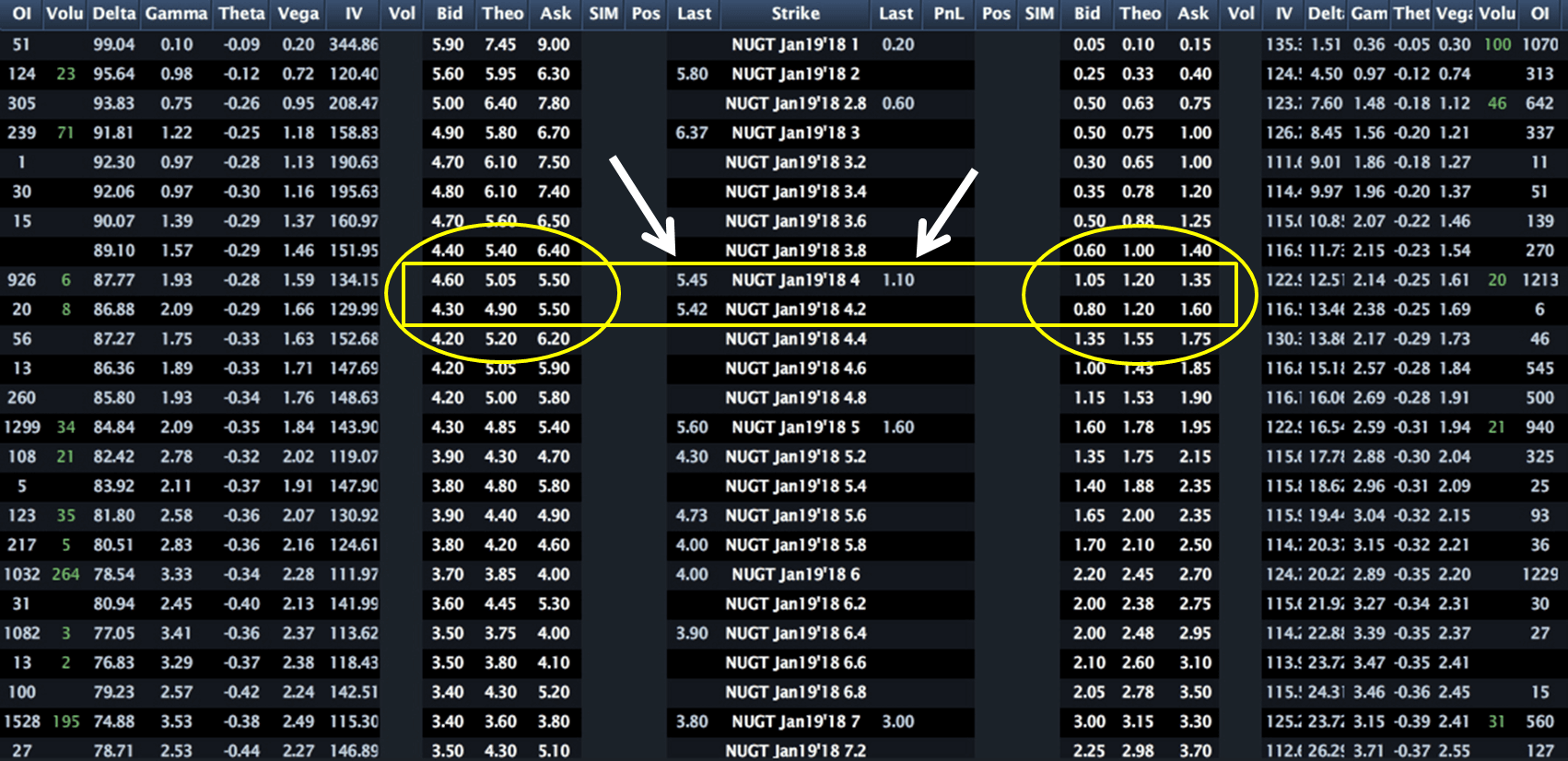
The yellow rectangle highlights the theoretical value and the bid/ask spread of the options, with calls displayed on the left and puts on the right. Within the ovals are the bid and ask prices for each option, with the bid on the left and the ask on the right. The theoretical value of each option lies between the bid and ask prices.
The white arrows point to the most recent trading price of the options, illustrating a variance between the theoretical value and the actual market price. It's crucial to remember that the market determines the price, not just the theoretical value.
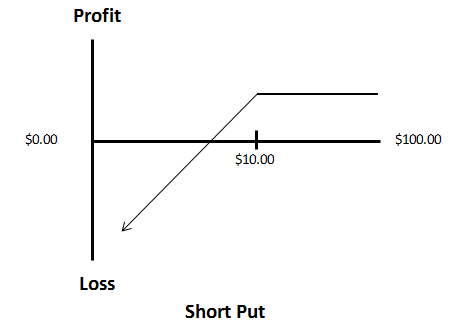
Now, let's examine the risk and reward associated with fundamental long and short positions. All scenarios will share the same variables: the stock price ranges from $0.00 to $100.00 per share, with a consistent $10.00 strike price in each example. To maintain simplicity, we will disregard time value in these illustrations.
The premium for each option remains constant at $3.00. It's important to note that each option grants the holder the right (or obligation) to buy or sell 100 shares of the stock.
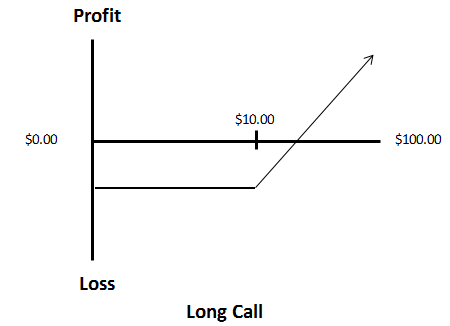
Long Call Position:
In this instance, we purchase a $10 call option and pay a $3.00 premium. The potential for profit is unlimited if the stock price rises; however, this gain would need to offset the premium paid. Conversely, if the stock price decreases, our maximum risk is limited to the premium paid for the option.
While the concepts discussed may seem straightforward, there are a few key points to consider.
When purchasing deep in-the-money call options, their movement closely mirrors that of the underlying stock, making them highly dependent on Delta. Conversely, at-the-money and out-of-the-money call options are more impacted by factors such as Theta and Vega.
Short Call Position:
In this scenario, the risk involved is unlimited, while the profit potential is capped at the $3.00 premium received. It's worth mentioning that personally, I have never engaged in naked call writing nor do I intend to do so in the future. The inherent risk outweighs the limited income potential. For instance, imagine being uncovered with short calls on a stock that unexpectedly announces an acquisition before the market opens – this scenario exposes one to significant overnight gap risk.
Here's a breakdown of the risk-reward trade-off:
If the stock indeed rises to $100, our potential loss would amount to $97.00, considering the $3.00 premium received upon selling the call option.
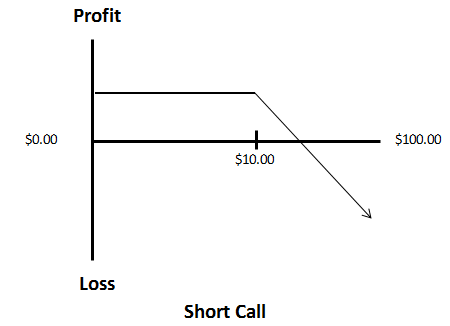
If the option closes at a price even one cent above the strike price, you be assigned the stock position.
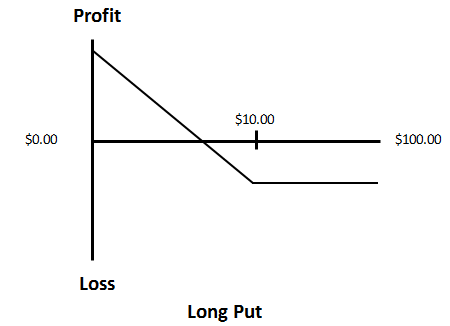
Long Put Option:
Owning a put option restricts both potential gains and losses, primarily because a stock's value can't fall below zero. In the event that the stock price reaches zero, the maximum profit achievable would be the difference between the strike price and the premium paid for the put option. Conversely, in the case of a stock price increase, the overall risk is capped at the premium paid for the put option.

The short put position is a bearish strategy that thrives on elevated implied volatility and a decrease in the underlying stock price. With a negative Theta, time is not in favor of this trade. Holding this position until expiration and having the option close even slightly in-the-money will result in being assigned the stock position and being short 100 shares.
The long call position is a bullish strategy that profits from an upward movement in the underlying stock price. It also gains from a reduction in implied volatility and boasts a positive Theta. Should the option expire even slightly in-the-money, automatic exercise occurs, resulting in a long stock position.
The following lesson will delve into some of the technical indicators that I consider before initiating an options trade.
