I've often heard people say, "I used to trade options, but I kept losing money." When I respond with, "You should have paid closer attention to the Greeks," I usually receive blank stares or silence, showcasing a lack of understanding.
Comprehending the option Greeks is crucial for managing the risk associated with option trades. These metrics provide insights into how an option's price will change concerning factors like time, price movements, and volatility. Mastering these concepts and implementing sound risk management practices can significantly enhance your success as an options trader.
Novice traders often buy calls expecting stock prices to rise or purchase puts when anticipating a drop. However, an option's price is influenced by more than just the stock price. Sometimes, despite a stock's upward movement, a call option may not increase or may even decline, leading to confusion. This phenomenon is often attributable to one or more of the Greeks.
The five primary Option Greeks are Delta, Gamma, Theta, Rho, and Vega. While Rho's impact is typically negligible unless dealing with long-term options, Delta's significance cannot be overstated. Delta indicates how much an option's price will shift with a $1.00 change in the underlying stock price.
Understanding Delta is vital. It ranges between 0 and 100 for calls and -100 to 0 for puts. A Delta of 0 occurs when the option is deep out-of-the-money or expiring imminently. As the option nears the at-the-money point, Delta increases for calls and decreases for puts. At-the-money options usually have a Delta around 50 (-50 for puts), with Delta climbing for calls as the stock price rises and declining for puts as it falls. Ultimately, Delta reaches 100 (or -100 for puts) for deeply in-the-money options.
Upon expiration, an option will settle with a Delta of 100 if it closes slightly in-the-money for calls and -100 for puts under similar circumstances. Understanding and applying these principles can significantly enhance one's options trading success.
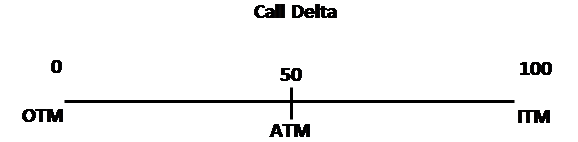
As depicted in the graph above, the call Delta transitions from zero when the option is out-of-the-money, progresses to 50 at the at-the-money point, and can max out at 100 when deep in-the-money. Conversely, the graph below illustrates a similar progression but in reverse for put options.
Delta is represented in percentage terms. For instance, a 50 Delta indicates that an option's premium will change by 0.50 for every $1.00 movement (up or down) in the underlying stock price. In simpler terms, an option with a 50 Delta will adjust by $0.50 for each one dollar shift in the underlying stock price.
The significance of Delta lies in its resemblance to the behavior of an actual stock: the higher the Delta, the more the option mimics stock movements.
Unlike a logarithmic progression, Delta moves from 0 to 100 (or -100 for puts) in a non-logarithmic manner. The rate at which Delta changes is influenced by another Greek known as Gamma.
Gamma pertains to how Delta is expected to alter (the 2nd derivative of Delta for those inclined towards calculus) for every $1 change in the underlying stock price. It serves as an indicator of the potential celerity of Delta's variation. A larger Gamma implies that the option's Delta will change more rapidly.
Similar to Delta, Gamma is expressed in percentage terms. For example, an option with a 25 Gamma would see its Delta adjust by 0.25 for each $1.00 movement (up or down) in the underlying stock price. The forthcoming examples will provide clearer insights into how Gamma influences Delta.

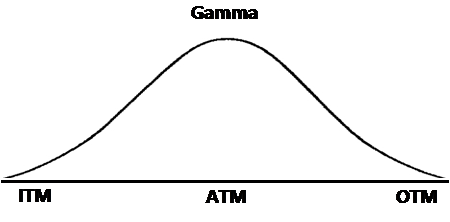
Gamma remains consistent for both put and call options, displaying a positive value for long positions and a negative value for short positions. It fluctuates in tandem with the movements in the underlying stock price and peaks when an option is at-the-money. As the option moves further into either in-the-money or out-of-the-money territory, Gamma diminishes.
As previously noted, there are situations where an option's value can decrease even if the underlying stock moves favorably (up for a call or down for a put). This phenomenon intensifies as the option approaches its expiration date, leading to faster erosion of value. This scenario exemplifies the impact of yet another Greek factor.
Theta pertains to the makeup of an option's price, composed of intrinsic value and time (extrinsic) value. As an option nears expiration, the extrinsic value diminishes at an accelerated pace, denoted by the option's Theta. It signifies the magnitude of time value that will dissipate in the following day.
With each passing day closer to expiration, Theta amplifies, with this escalation occurring exponentially. The following example illustrates how Theta can deplete an option's time value.
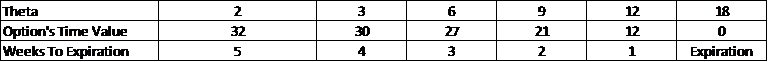
Now, let's visualize this scenario on a graph.
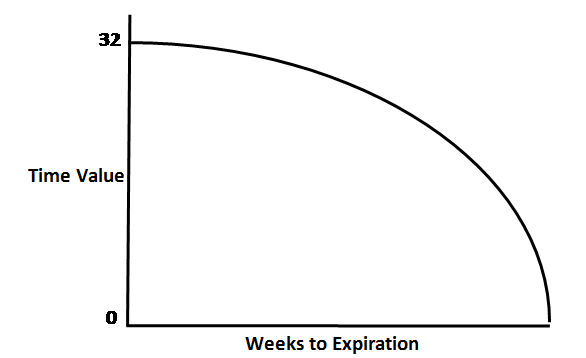
When you buy an option (either a call or a put), your position carries a negative Theta. Conversely, when you sell premium (via a call or put), you possess a positive Theta. Theta works against an option buyer, while it works in favor of an option seller.
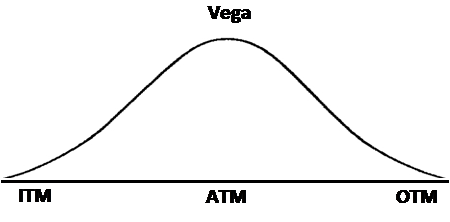
Vega quantifies how much an option's price is anticipated to fluctuate in response to a one-point alteration in the Implied Volatility of the underlying stock. For instance, with a Vega of 0.25, an option would shift by 25 cents when the underlying stock's implied volatility changes by 1 point. Below are examples to elucidate this point further.

Vega remains consistent for both puts and calls, being most responsive when an option is at-the-money.
When you purchase an option, whether a call or put, your position exhibits a positive vega. An increase in implied volatility works in your favor. Conversely, sellers of premium gain from a reduction in option volatility due to their negative vega position.
Next, I will delve into how options can be strategically utilized to meet particular investment goals.
